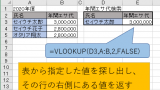
エクセルには、表から値を探し出し、その右側にある内容を表示する事ができる、VLOOKUP関数というものがあります。(下記記事参照)
そしてこのVLOOKUP関数には、注意書きがあります。あまり気にしてる人は多くないと思いますが。
テーブルは昇順で並べ替えておく必要があります。
なぜこのような注意書きがあるのかというと、VLOOKUP関数が表から値を探す際、表の上から順に探しにいく。という動きをしているためです。
どういう事なのかを実験しつつ、どういった問題が起こりうるのかなども考えてみましょう。
また、VLOOKUP関数の式は=VLOOKUP(検索値,範囲,列番号,検索方法)となっており、検索方法にはTRUE(完全一致)とFALSE(近似値)の2種類がありますので、それぞれの特徴についてもお話していきます。
検索方法FALSE(完全一致)
VLOOKUP関数を使う際、多くの場合はこのFALSE(完全一致)を使うことになるでしょう。
なので、まずはこのFALSEの動作について実験していきます。
FALSEの挙動
検索値を表の上から探し出して、その右側にある値を結果とします。
どういう事が順を追ってみていきましょう。
まずは普通に使ってみます。
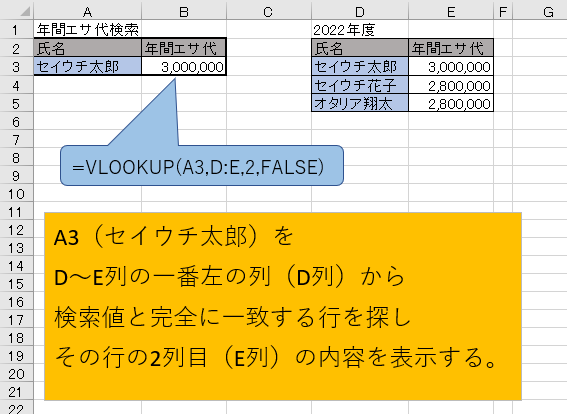
表からセイウチ太郎を探してエサ代を表示するという、いたってシンプルな使い方ですね。
次は、セイウチ太郎を探す際、本当に表の上から順に探しているのかを実験してみましょう。
どういう実験かというと、検索先の表に、複数のセイウチ太郎を用意し、何番目のセイウチ太郎が選ばれるのかという内容。
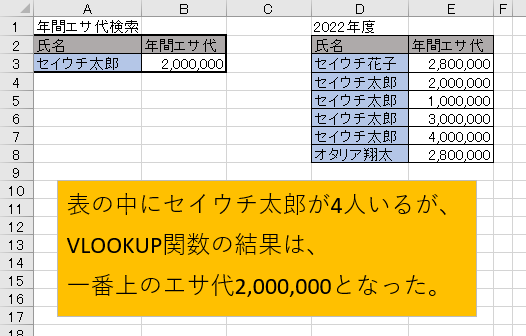
結果は、表にセイウチ太郎が複数名いても、VLOOKUP関数が拾ってくるセイウチ太郎は、上から探して1番目に見つけたものでした。
昇順で並べなくてはいけない?
注意書きにあった、テーブルは昇順で並べ替えておく必要があります。の一文についてですが、仕組みさえわかっていれば、FALSE(完全一致)での検索の場合は、絶対順守ではありません。
むしろ下図のように、使い方次第では昇順の逆、降順にする事で有効活用できる場合もあります。
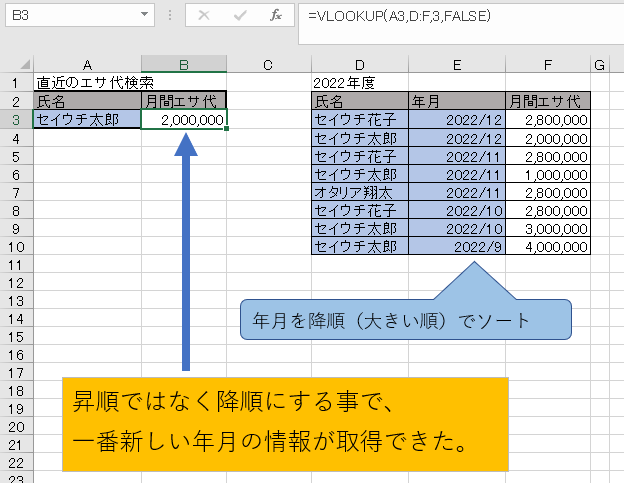
このケースで年月を昇順にしてしまったら、逆に一番古い情報、2022/9の4,000,000円という結果になってしまいます。
このように、仕組みさえわかっていれば、絶対に昇順にしなくてはいけない・・・というわけじゃないって事ですね。
ただしこれは完全一致で検索した場合のお話で、近似値検索になるとまた話は変わってきます。
検索方法TRUE(近似値)
ちょっと隠れがちな存在ですが、覚えていると、いざという時にとても便利な近似値検索について。
TRUEの挙動
完全一致検索の、表の上から順に探しだすという動きとは全く違う動きをします。
まず完全一致の時と同様、検索値と同じ値がちゃんと表にもある場合。

続いて近似値を活かすために、表中に存在しない値を探す場合。
たとえば61点を近似値検索するとどうなるか試してみましょう。

60点のがんばれが結果になりました。
61の近似値という事で、一番近い60点が選ばれたのかな・・・と思われそうですが、実際は違います。
どういう事かを試すために、60に近い61ではなく、80に近い79を検索してみましょう。

79が一番近い表中の数値は80ですが、80点のもういっぽは選ばれず、60点のがんばれが結果となりました。
なぜこうなるのかは、近似値検索の場合は、二分探索するという動きが関わってきます。
エクセルがどういう挙動をしてこの結果になったのか、順を追ってみていきましょう。
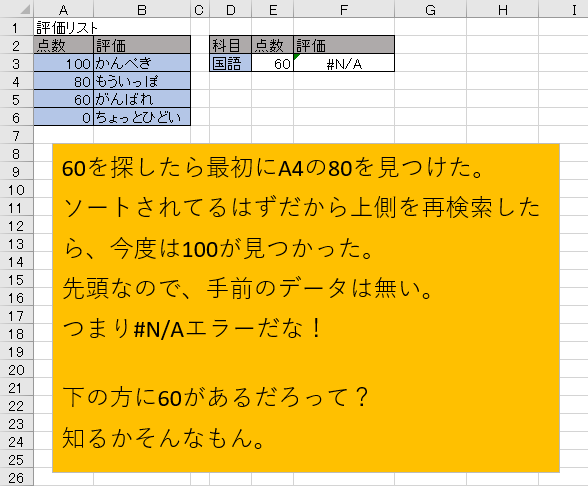
あと、二分探索の説明の都合上、検索範囲を列全体ではなく、範囲を絞った式を使います。
式:=VLOOKUP(E3,A3:B6,2,TRUE)
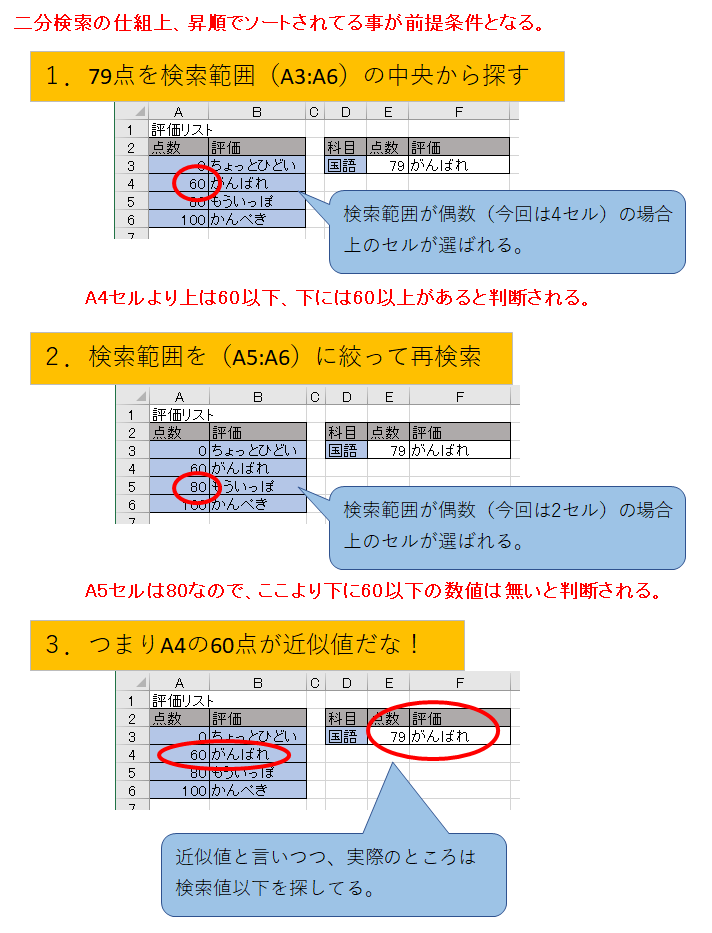
注意すべきは、近似値検索と言いつつ、実際は検索値以下を探しているという事。
まず、範囲をA3:B6にしているので、検索範囲としてはA4:A6を検索するように動きます。
次に、A3~A6の中央セル、A5セルが最初にチェックされます。
先頭から順に検索していく完全一致との大きな違いはここで、二分探索はスタートが中央からとなります。
そしてA4セルは60なので、79以下という検索条件を満たしています。
なので、A4セルより上にはもっと小さい数値しかなく、A4セルより下にはまだ79以下の数値があるかもしれないと判断されます。
なぜそう言い切れるのかって、VLOOKUP関数の注意書きに、テーブルは昇順で並べ替えておく必要があります。という一文がありますよね?
つまり、この前提条件を守らないと、そもそもうまく機能しないという事になるんです。
さて、次は範囲を狭めて、A5~A6セルを検索範囲とし、再び中央セルの値をチェックします。
今度の中央セルは、A5~A6の中央なので、A5セルが対象となります。
そしてA5セルの値は80で、小さい順に並んでいるのだから、この先に79は存在しない。と判断します。
つまり79の近似値は80よりも手前にいるはず・・・
そうか60点!お前が79点の近似値だな!
となります。
えぇ・・・近似値って言うたやん・・・それじゃあ以下やん・・・って思う人もいるでしょうが、しょうがないじゃない、そう動いてるんだもの。
試しに昇順ソートを崩して、80点と60点を入れ替えてみましょう。
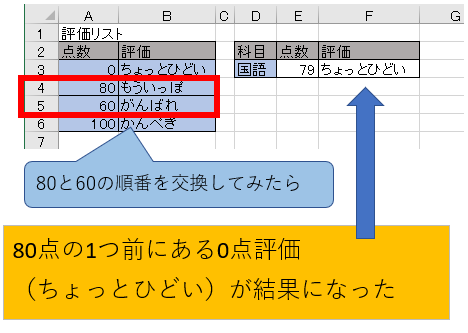
ほら、最初の検索で80を見つけたから、次は範囲を狭めたら(っていうかA3セルのみですが)、A3セルの0点を近似値として拾ってきたのだから、間違いないです。
さて、途中にちょいちょいと二分探索という言葉が出てきました。
こいつがどういう動きで検索しているのかを書いてみましたので、興味ありましたらぜひご覧ください。

理解していれば便利
このように、検索方法TRUE(近似一致)の場合、ちょっとクセの強い動きをします。
ですが、仕組みさえわかってしまえば、けっこう実用的なんです。
実際にここまでの例で使ってきた表がまさに、点数次第で評価を分けるというもので、私自身、これに近い使い方をよくしています。

わざわざIF関数で、59以下ならC、79以下ならB・・・みたいに、やたらと長い式組んでる人もいますからね。
近似値検索の場合は昇順ソートをすべき
完全一致の場合は、昇順ソートは絶対に必要というわけではないと書きました。
ただし近似値検索の場合、昇順ソートされていること前提のロジックで動いているため、何か意図が無い限り、昇順ソートは必須と言えます。
誤って降順ソートしてしまうと、全く思った結果にならないという事も。
ね?
数値以外の場合も基本は同じ
検索値が数値の場合はわかりやすいのですが、それ以外の場合も考え方は同じです。
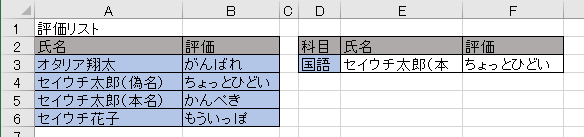
Bを検索すると、Cは行き過ぎで、Bより手前のAを拾うみたいな。

セイウチ太郎(本 よりセイウチ太郎(本名)の方が大きいから手前のセイウチ太郎(偽名)を拾うみたいな。
まとめ
検索方法がFALSEの時は状況次第、TRUEの時は昇順ソートしよう。



コメント