MATCH関数とは
MATCH関数は、検索したい文字列指定を、検索範囲から探し出し、それが何行目(何列目)かを返す関数です。
公式説明では下記のようになってます。
わかりにくいですね。
検索したい文字列が何番目のセルで見つかるかを調べる関数と覚えておいて問題ないです。
MATCH関数の使い方
式:=MATCH(検索値,検索範囲,照合の種類)
検索値はその名のとおり、検索したい文字列や数値を入力します。(セル参照もOK)
次の検索範囲は、検索値を探す範囲を指定します。
この時、複数行・複数列を指定するとうまく動作しないので、A:AやA1:A5、1:1やA1:E1のように、1行(1列)になるように指定しましょう。
最後に照合の種類ですが、以下・完全一致・以上の3パターンが指定できます。
以上が1、完全一致が0、以上が-1となっており、省略すると以上(1)が指定された事になります。
0を指定して使う事が多いと思いますので、指定忘れに気をつけましょう。
MATCH関数を使ってみる
実際にMATCH関数を使ってみましょう。
完全一致
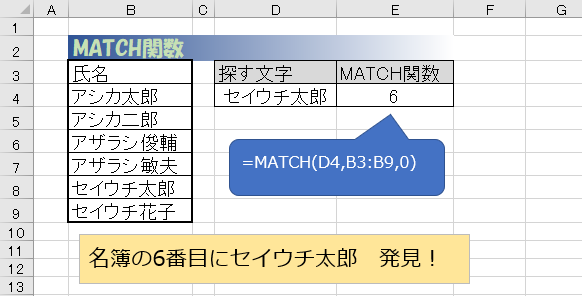
試しに、名簿の氏名からセイウチ太郎を探し、何行目にいるかを探し出します。

A列を上から順に探していった結果、6行目にセイウチ太郎を見つけたので、結果は6となりました。
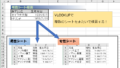
ちなみに縦方向ではなく横方向(何列目かを調べる)にする場合は下図のようになります。

2行目を左から順に探していった結果、4列目に〇印を見つけたので、結果は4となりました。
以下(照合に1を指定)
処理の都合上、事前に表を昇順(小さい順)ソートしておく必要があります。
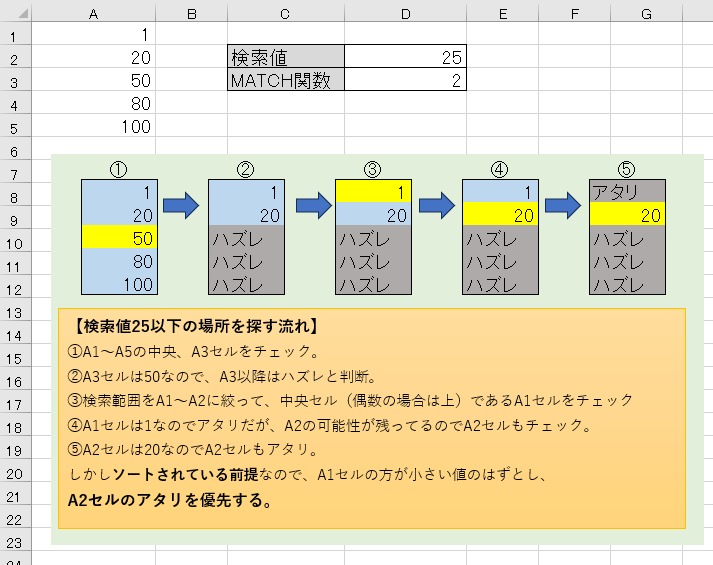
今回は1,20,50,80,100の順に並んでいるデータから、25を探してみましょう。
すると、25以下の数値、20が検索結果だと判断され、結果は2行目で見つかった事になります。

この時、検索の仕方は上から順に条件に当てはまるセルを探していくわけではなく、二分探索という探し方をしています。
ザックリ言うと、ソートされている事を前提として、全体の真ん中を調べて、その結果で次の検索範囲を半分に狭めて、また真ん中を調べてを繰り返す動きです。
どう動いてるのか細かい部分まで知りたい方は二分探索の記事をご覧ください。

今回の場合はこんな感じ。
以上(照合に-1を指定)
処理の都合上、上から順に検索値を探し、検索値より小さい値を見つけた場合、1つ前を結果とするため、事前に表を降順(大きい順)ソートしておく必要があります。
今回は100,80,50,20,1の順に並んでいるデータから、25を探してみましょう。

まず上から順に100,80,50,20と探していき、4行目で25より小さい20を見つけます。
20は25よりも小さいため、それよりも1つ前の50が、25以上の検索結果だと判断され、結果は3行目で見つかった事になります。
完全一致ではワイルドカードが使える
照合を完全一致にした場合、ワイルドカードを使う事ができる。

ア*太郎は、アと太郎の間に何が入っていても良いので、アシカ太郎が引っかかり、結果は2行目となる。
同じくセ*太郎は、セと太郎の間に何が入っていても良いので、セイウチ太郎が引っかかり、結果は6行目となる。
そしてア???太郎は、アと太郎の間に3文字分の何かが入っていれば良いことになるので、アザラシ太郎が引っかかり、結果は4行目となる。
ア???太郎のを検索した時、アシカ太郎ではアと太郎の間にあるのは2文字(シカ)だけなので、ア???太郎では検索に引っかからない。
以下・以上を指定したのに表のソートをしていないと
照合で以下・以上を使用する場合、事前に表を昇順・降順にする必要があると書きました。
ではそれを守らないとどうなるのか、実験してみましょう。
まずは照合に以上(-1)を指定したのに、表を昇順(小さい順)にしてしまった場合。
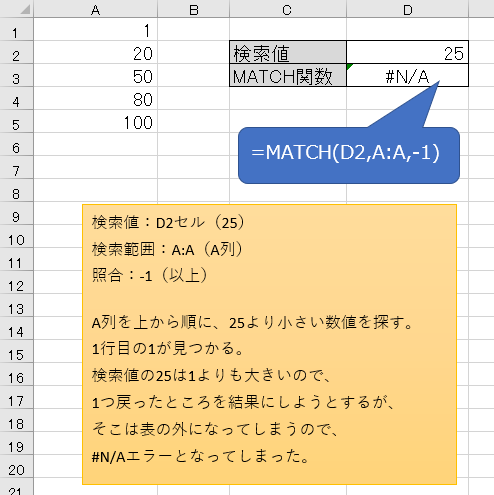
25より以下の数値を表の上から探すと、1行目の1が見つかる。
25は1よりも大きいため、1つ前の行が正解だと判断されるが、1行目より前の行は存在しないため、#N/Aエラーとなってしまいました。
続いてその逆、以下(1)を指定したのに、表を降順(大きい順)にしてしまった場合。
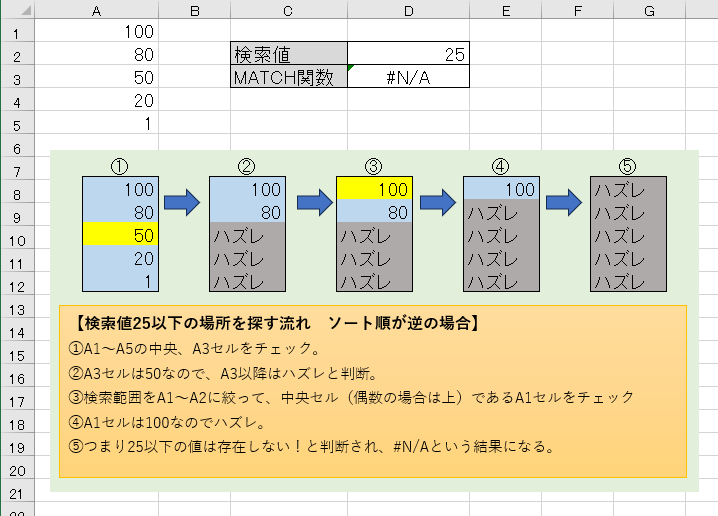
このように、検索範囲を半分、半分に絞っていった結果、25以下の値が見つからずに#N/Aという結果になってしまいました。
ここで面白いのは、検索のスタート位置が中央セル(今回はA3)なので、中央セルが条件を満たしている場合は、それ以前のセルが条件を満たしていなくても、検索が続行されます。

更に言うと、検索値と完全一致セルを見つけたか、一致ではないが条件を満たしているセルを見つけたかで動きが変わるので、似たような表でも結果が変わる場合もあります。

以上の事からわかるように、以上・以下の検索を使う場合は、あらかじめ表をソートしておきましょう。
もちろん、動きを理解しているうえで、意図的にソートしないというのは問題ありませんが、Googleのスプレッドシートと動きが違う部分があるようなので、同じファイルを開いたのにエクセルとスプシで結果が違っているなんて事になる可能性があるため、あまりオススメしません。
まとめ
表から検索値を探し出して見つけた場所を示す、名前の通りの機能をもった関数でしたね。
MATCH関数は単体だと使い方に悩むのですが、INDEX関数やVLOOKUP関数など、他の関数と組み合わせる事で可能性が広がる関数です。
例えば、=VLOOKUP("セイウチ太郎",A:E,MATCH("生年月日",$A$1:$E$1,0),FALSE)のように、生年月日の項目名を探し出してVLOOKUPの列番号を自動で拾ってくれるようにするなど。
他にも、やる事はVLOOKUPでも、INDEXとMATCHを組み合わせた方が処理が軽くできるなど。
式を組む時はちょっと悩むかもしれませんが、上手く使えば非常に効果のある式が作れますので、ぜひ挑戦してみてください。

コメント