エクセルでは、VLOOKUP関数で近似値検索(検索方法でTRUE)や、MATCH関数で検索値以下の最大値(照合の型で1)を指定した場合、上から順に検索値を探していくのではなく、全体の真ん中を調べて以上か以下を判断 を繰り返して検索値を探す、二分探索(バイナリサーチ)という動きをしています。
今回はその、二分探索がどういう挙動をしているのか、いろいろテストして仮定を立ててみます。
あと、最後の方で書きますが、XLOOKUP関数や、XMATCH関数でいうところのバイナリサーチについての解説ではありません。
というか、XMATCH関数らの方がしっかり二分探索していて、MATCH関数の方が亜種といった印象なのですが、とにかくこの件は後ほど。
はじめに
今回は実験にMATCH関数の照合の型:1(検査値以下の最大の値を検索、要は以下検索)を使用します。
また、当記事の実験では、正確な答えには辿り着きません。
だってマイクロソフトさんがソース公開してるわけじゃないですからね、あくまでも実験結果から仮定を立てるまでとなります。
二分探索とは
まずは二分探索がどういうものか、シンプルな例で動きを確認してみましょう。
例:検索の中から8以下を探す

このように、検索範囲の真ん中チェックを繰り返し、少しずつ検索範囲を狭めて、最終的に答えに辿り着くのが二分探索です。
上から順に検索値を探していくと、この例の場合ならば8を見つけるために8回の検索をする必要がありますが、二分探索ならば3回のチェックで完結しており、処理が軽いというメリットがあります。
そしてこの記事では、10件の真ん中は6じゃなくて5なの?、本当に一致する値を見つけたのに次のデータもチェックしてるの?といった、細かい疑問点を解決するための実験をしていく感じになります。
偶数件数の真ん中はどっち?
先ほど、10件の真ん中は5だと書きました。
これが本当かどうかを確認するために、3パターンのテストをします。
テスト
1.4番目が一致

2.5番目が一致

3.6番目が一致

まとめ
5番目が条件に一致した場合のみ、結果が#N/Aとならなかった。
10件の真ん中というと、5番目と6番目が候補になるが、この実験から、検索のスタート位置は5番目だという事がわかる。
つまり検索範囲が偶数である場合の検索スタート位置は、真ん中の上側だと予想できる。
式にすると範囲10÷2=スタート位置5となるから。とすれば覚えやすそう。
完全一致の挙動
検索値と完全一致した場合の挙動をいろいろ実験してみます。
テスト
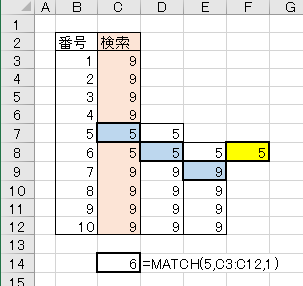
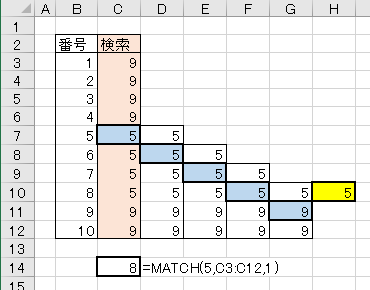
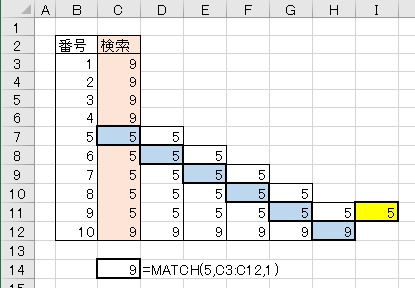
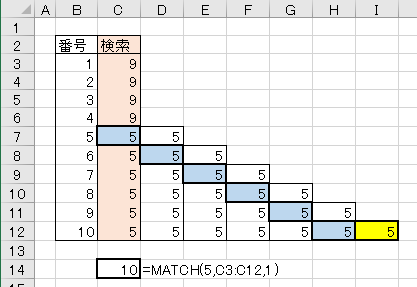
1.完全一致が連続した場合

2.完全一致の次が不一致で、また完全一致に戻る場合
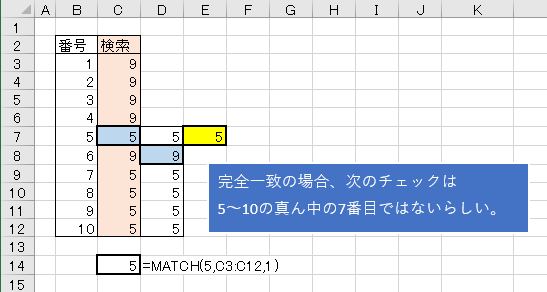
3.完全一致の前も完全一致の場合
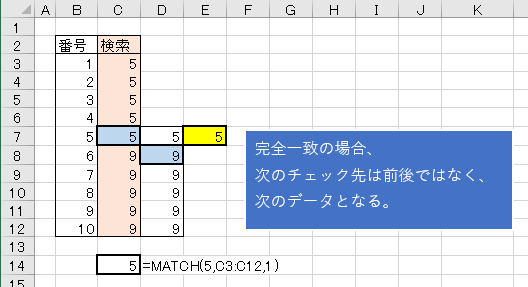
4.完全一致の次以降が条件一致の場合
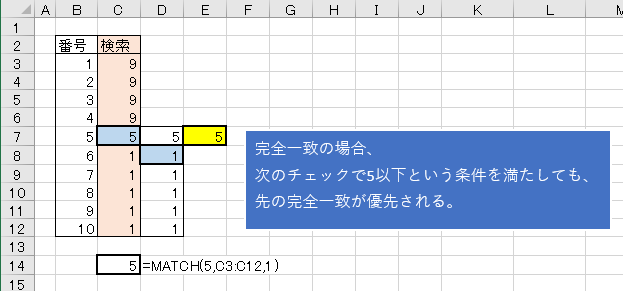
まとめ
二分探索は範囲を半分に、半分にを繰り返していくものだが、検索値と完全一致した場合は次のデータをチェックするのを繰り返しているようです。
また、完全一致の次のデータが条件一致(以下という条件は満たしているが、完全一致ではない)の場合、完全一致が優先される。
MicrosoftサポートのMATCH関数解説では、検査値以下の最大の値を検索します。となっているので、その通りの結果となりました。
2回目の検索範囲はどこ?
二分探索は、範囲を半分、半分と狭めていくというものです。
完全一致の場合は、次のデータをチェックするを繰り返してましたが、条件一致の場合は、範囲を半分に絞ってチェックをするように動いています。
というわけで今度は、2回目の検索範囲はどこ?という疑問を解決していきましょう。
テスト
今回のテストでは、完全一致の場合は探索を終了させやすいという特徴を利用していきます。
1.最初のチェックが条件一致の場合


2回目は何番目のデータをチェックしているのか確認するために、単独完全一致ならそこで探索は止まるという特徴を使ってみました。
その結果、2回目のチェックは、8番目のデータを見ているという事がわかりました。
これにより、2回目の検索範囲を決める時は、前回のチェック対象は除いているという事が予想できます。
つまり、5番目のデータをチェックした次は、5~10の中央(7番目)ではなく、6~10の中央(8番目)をチェックしている事がわかりました。
2.最初のチェックが条件不一致の場合
今回初登場、1回目のチェックが条件不一致で、次の検索が上の方になる場合のテストです。
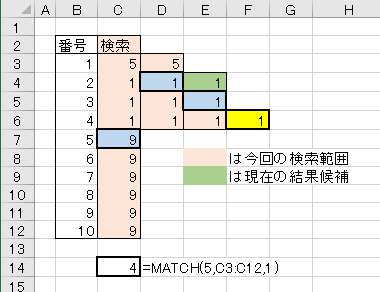
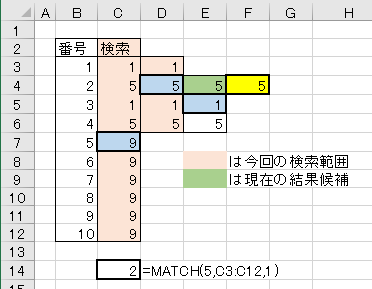
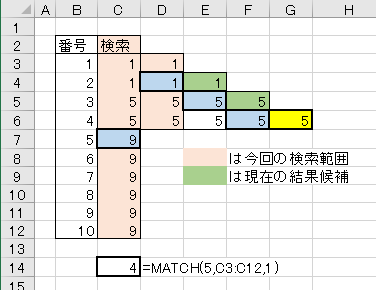
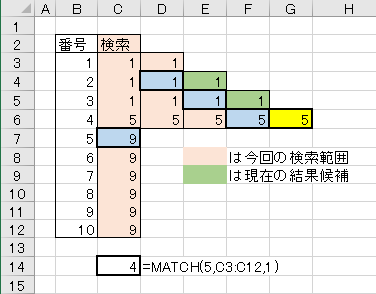
これらの結果から、1回目チェックが条件不一致の場合でも、2回目以降の検索範囲を決め方は同じルールが当てはめられるという事がわかりました。
まとめ
2回目以降の検索範囲を決める時は、前回のチェック対象は除いて範囲を決め、その中央のデータをチェックし、また次の検索範囲を決める。
これを、答えが出るまで繰り返しているという事がわかりました。
空欄の扱いはどうなる?
チェック対象が空欄の場合はどうなるでしょう。
テスト
1.不一致と同じ動きか
空欄が以上扱いになる事は無いでしょうから、不一致の以下(0扱い)になるのかを確認。
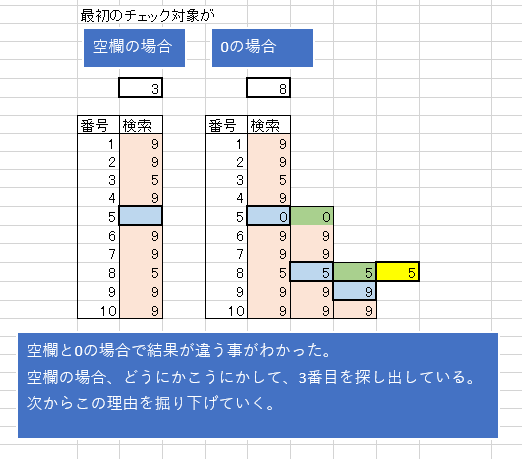
この結果から、空欄と0は別物扱いという事がわかる。
そして、結果が3番目となっている事から、最初のチェックでは検索値を超えていると判断された事がわかる。
そこで、空欄の場合は検索対象を一つ下げているのではないか。という仮説を立てて実験していきます。
今回の場合5番目が空欄なので、6番目の9が最初のチェック対象となったのでは?という事。
2.空欄の場合チェック対象が1つ下になる場合の動き
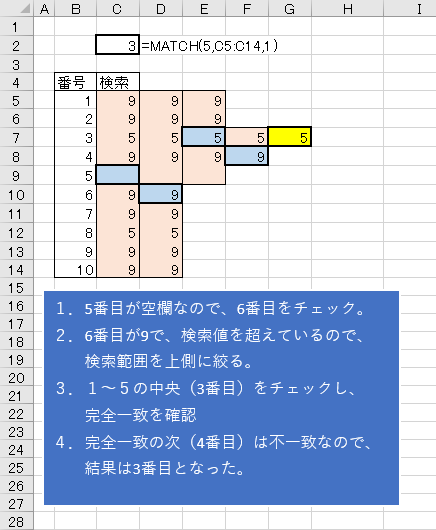
これなら結果が3になった理由に納得できます。
3.空欄が続く場合
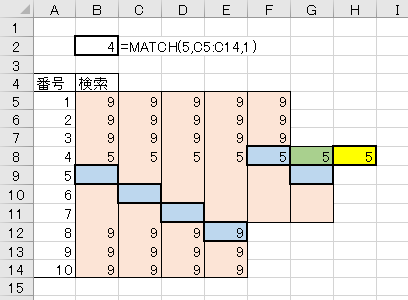
この結果から、空欄が続く場合、何か値を見つけるまで下に進み続け、値を見つけたところでチェック。
そして次の検索範囲には空欄も含めており、その範囲の中央を次の検索位置としている事がわかる。
それを証明するのが下のパターン。

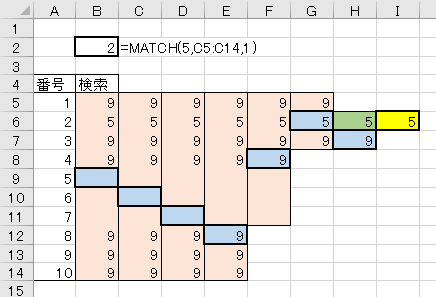
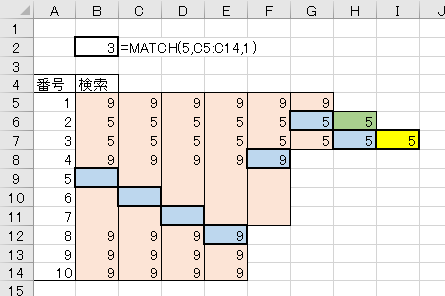
4.最初のチェック対象が一致(検索値未満)の場合
検索範囲を下側に狭めていく場合、想定通りに動いているか実験してみましょう。

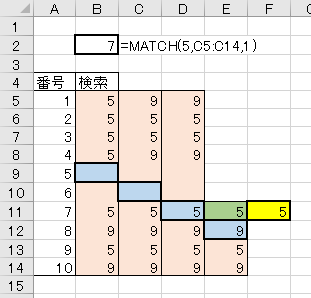
5.最初のチェック位置含め、それより下が全て空欄の場合
要は下半分が全部空欄だったらどうなんの?って事。

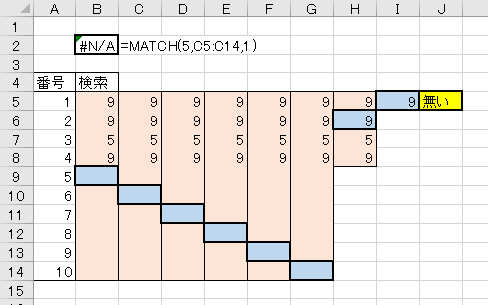
先が全部空欄だったら、最初のチェック対象を未満として扱って上側に検索再開するようですね。
6.2回目以降のチェック対象が空欄の場合
初回チェックが空欄の場合にどう動いているかは、まだ言語化できるのですが、2回目以降についてはなんかこう、感じ取ってください。
だいたい想定している動きではあったのですが、こんなん文章にできるか!って結果になりました。
人によっては、あーそっちが優先されるのかーって思うかもしれません。
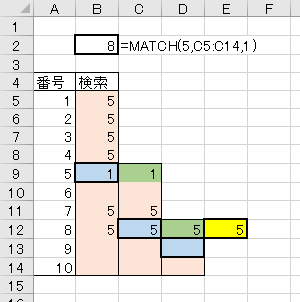
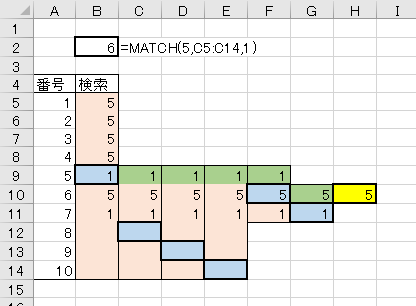
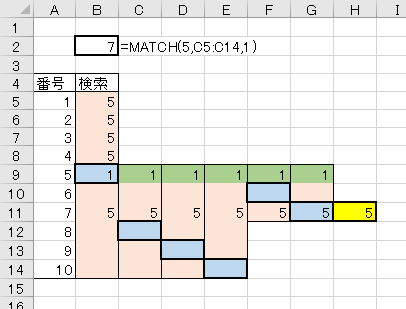
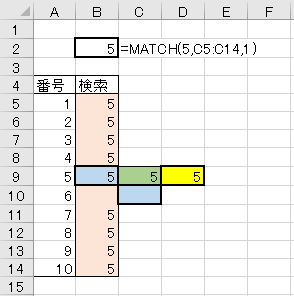

少し複雑にして、下方向、上方向、からの空欄発見といったパターンもテスト。

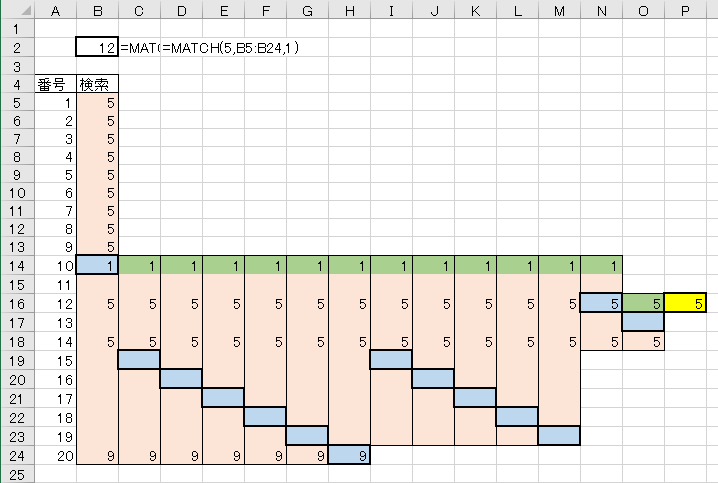

まとめ
色々試してみた結果、チェック対象が空欄の場合、1つずつ下に移動している事がわかりました。
あと、チェック対象以降が全部空欄の場合は未満とみなし、検索範囲を上方向に絞って仕切り直してますね。
ただし、2回目以降のチェックで空欄を引き当てた場合は、前のチェック結果が影響する事で混乱しそうになる。(完全一致としての挙動が優先されるなど)
あと、ここでは空欄の場合としてテストしてきましたが、正確には違うようです。
これについては次の項目で。
さっきの動きは空欄の場合ではなく、データ型が違う場合だった
空欄の場合はどうなるんだろう?という入り方で、一つ前のテストをしてきました。
ですが、空欄の場合ではなく、数値を二分探索しているのに、次のチェック対象が文字列だった場合といった、データ型が違う場合の挙動だったという事がわかりました。
それを確認するためのテストがコチラ。

このように、2回目のチェックで数値として未満・完全一致・超過の結果と、空欄・文字列での半角数字・全角平仮名は結果は、別の答えが返ってきました。
そして、空欄・文字列での半角数字・全角平仮名は同じ結果になっていますので、空欄かどうかではなく、データ型が同じかどうかで、動きが変わっているという事がわかりました。
ソートした時、数値の1より漢字の壱の方が大きい扱いだから、二分探索でも超過と同じ扱いになるんやろな!って思いこんではいけないという事ですね。
また、二分探索を使う時に、あらかじめソートが必要だとなっていますが、数値の1と文字列の1が混ざってるような状態では、事故が起きる可能性があるという事もわかりますね。
念のためですが、データ型が同じならば、思ったような二分探索をしてくれますので、数値じゃないとダメってわけじゃないですからね。
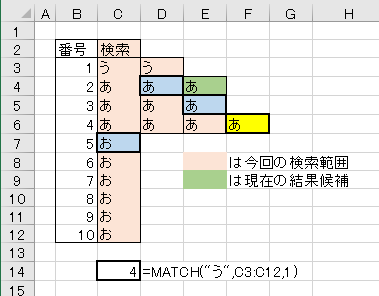
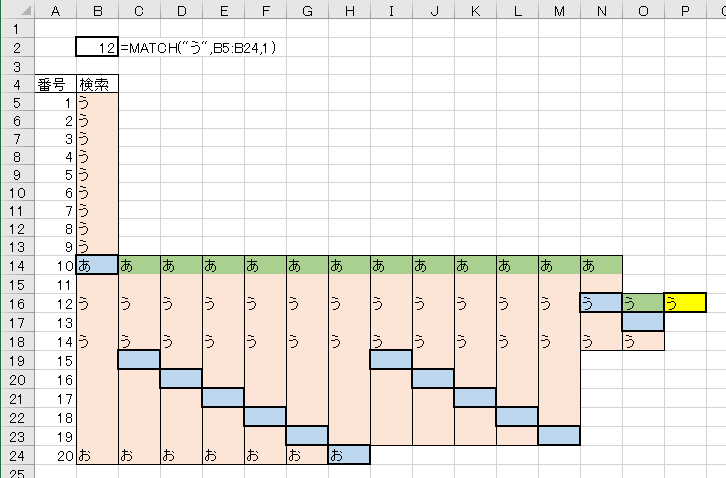
あいうえお順のテスト、見た目がややこしくて頭が混乱する。
二分探索の動きを整理すると
動きについて
ここまでの実験で、エクセルでの二分探索は、基本は以下のような動きをしていると予想できます。
- 検索範囲の真ん中にあるデータをチェック(検索範囲が偶数なら1つ上が選ばれる)
- 完全一致の場合は次のデータとの比較を繰り返す
- 検索値未満なら下方向、超なら上方向を探索していく
- 次の検索範囲を決める時は、前回チェック対象となったデータは除く
- データ型が違う場合はチェック対象を次のデータにする
- これを繰り返し検索範囲を狭め、最後の1つになったところが答えとなる
ただ2回目のチェック以降で別データ型を引き当てた時の動きが言葉では表現しにくいので、感覚で悟ってください。
メリット
メリットはやはり、処理の速さですね。
MATCH関数やVLOOKUP関数で完全一致検索をすると、上から順にチェックしていくように動きます。
対して、VLOOKUP関数の近似一致や、MATCH関数の以下の最大の値検索を指定する事で、この二分探索を使うようにすると、検索範囲を半分→半分→半分・・・という動きをするため、結果としてチェック処理の回数が減り、処理が軽くなります。
データ件数が少なければ大差ありませんが、データ件数が膨大であるほど、効果は絶大になります。
あとはVLOOKUP関数の近似一致とかで、1点~5点なら評価B、6点以上なら評価Aみたいな使い方ができるのも利点。
具体的な使い方はこちらをご覧ください。

デメリット
ちゃんとデータ郡をソートしておかないと、思うような結果が返ってこない事があります。
二分探索を理解せずに、処理が速いっていうからとりあえず近似一致にしといたー。
なんて軽い気持ちで使うと、思わぬレコードを拾ってきてしまったり、存在するはずのデータが見つからないなどの事故に繋がりますので、なんとなくでも、どう動いてるのかを理解して使いましょう。
上から順に見てるんじゃないんだなーっとだけでも覚えておけば、あらかじめソートしておく重要さにも気づけるはずでしょうから。
正直なところ僕自身も、ほんとに細部までは理解しきれてないのですが、ソートする事さえ守っていれば、今のとこ大きなトラブルにならずに済んでますんで、そこまで難しく考えなくてもなんとかなるなる!
これ二分探索なの?
ここまで、VLOOKUP関数とMATCH関数における二分探索についてのテストだ!と言い張ってきましたが、正直なところ、二分探索のようなものという印象。
まずこの二分探索がどういうアルゴリズムなのか、概要をWikipediaより引用してみましょう。
ソート済みのリストや配列に入ったデータ(同一の値はないものとする)に対する検索を行うにあたって、 中央の値を見て、検索したい値との大小関係を用いて、検索したい値が中央の値の右にあるか、左にあるかを判断して、片側には存在しないことを確かめながら検索していく。
引用 Wikipedia - 二分探索
中央を見て検索範囲を狭めていく。
うん、さっきまでテストしてた二分探索がまさにこれですね。
・・・あれ?
空欄の場合(データ型が違う場合)の動きであった、次のセルを見るなんて動きについて触れてないよね?
というわけで僕の中では、VLOOKUP関数とMATCH関数における二分探索は、ほぼ二分探索という認識になりました。
そうすると今度は、世間で言うところの二分探索とはちょっと違うけど、エクセルでの二分探索って言ったらこう動いてる。っていう話じゃないの?という疑問が出てきます。
これについては、XLOOKUP関数と、XMATCH関数によって否定できます。
このXLOOKUP関数とXMATCH関数は、一致・未満・超過の指定とは独立して、検索方法が選べるようになっており、そこでバイナリ検索(二分探索)を選べるようになっています。
で、実際に二分探索を選択して、同じような条件でMATCH関数とXMATCH関数を動かすとですね・・・
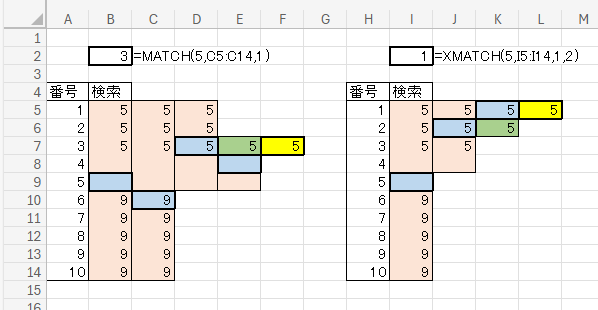
このように、結果が違うんですよね・・・。
この結果から、XMATCH関数での二分探索では次の値を見るという動きはしておらず、こっちの方が純粋な二分探索をしているという事がわかります。
つまり、エクセル内ではVLOOKUP関数やMATCH関数で近似一致指定をした場合は二分探索するよ!と言われているものの、厳密にはほぼ二分探索をしていて、XLOOKUP関数やXMATCH関数でのバイナリ検索指定こそが、ちゃんとした二分探索なんじゃなかろうかと。
まぁなんにせよ、ちゃんとデータ型を合わせてソートした表を用意さえしていれば何も問題はないって話なので、ルールを守って正しく関数を使いましょうねの一言に尽きます。
以上、知っておくと思ったような結果が出なかった時に原因が探れるようになる豆知識でした。
おまけテスト
出番の無かったテスト結果をここに供養しておきます。

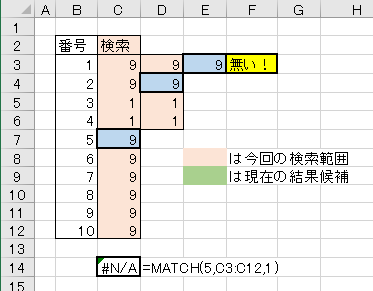
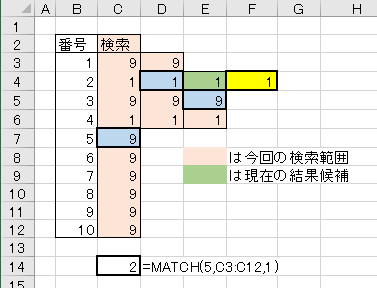



コメント